Anscombe’s quartet is a set of four toy datasets that look very different, but many of their statistics coincide. They were developed by Francis Anscombe as a striking visual to show that even for small datasets, blindly examining their statistical properties without considering their structure can mislead.
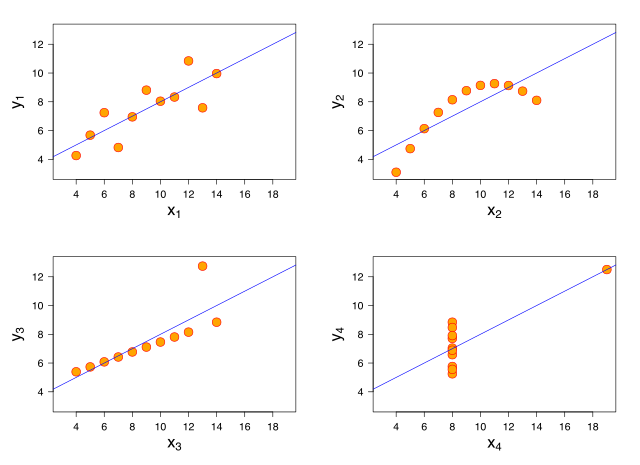
Particularly, the four datasets have the same least squares regression line. While the second dataset is a clear example of a nonlinear correlation which cannot be accurately captured by any linear model, the third dataset is actually perfectly linear, with no noise, but just a single outlier that shifts the regression line considerably.
Support vector regression is an extension of the support vector machine idea to tackle the regression problem. It is based on the observation that a SVM classifier builds its decision boundary as a function of a (small) subset of training points. For regression, SVR fits a tube that is robust to noise within a width [latex]\epsilon[/latex]. For this particular example, using a small width makes the solution robust to the obvious outlier. For very small but non-zero [latex]\epsilon[/latex], the solution is a combination of the outlier and on two other points. For [latex]\epsilon=0[/latex], you can see that every point except a non-outlier is highlighted. This is actually the perfect solution but very dense.
[
][]
Every frame displays the global mean squared error and the true mean squared error, i.e. over the inlying points. If the epsilon size is well chosen, SVR can perform robustly with a sparse solution. Since our interest was in avoiding the outlier, we assumed no noise in the inlying data, so a very small epsilon is perfect. For real data a larger epsilon is often useful because of variability in the data. When adding noise, SVR still manages to avoid the outlier, but when the tube width becomes zero, the solution is again very dense, very non-parametric.
[
][]
Here is the code you can use to play around with this.
[gist id=2815589]
[]: http://localhost:8001/wp-content/uploads/2012/05/svr.gif
[]: http://localhost:8001/wp-content/uploads/2012/05/svr_noise.gif
Comments !